Stirling number
In mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second kind.
Contents |
Notation
Several different notations for the Stirling numbers are in use. Stirling numbers of the first kind are written with a small s, and those of the second kind with a large S (Abramowitz and Stegun use an uppercase S and a blackletter S respectively). Common notations are:
The notation of using brackets and braces, in analogy to the binomial coefficients, was introduced in 1935 by Jovan Karamata and promoted later by Donald Knuth; it is referred to as Karamata notation. (The bracket notation conflicts with a common notation for the Gaussian coefficients.) The mathematical motivation for this type of notation, as well as additional Stirling number formulae, may be found on the page for Stirling numbers and exponential generating functions.
Stirling numbers of the first kind
Unsigned Stirling numbers of the first kind
(with a lower-case "s") count the number of permutations of n elements with k disjoint cycles.
Stirling numbers of the first kind (without the qualifying adjective unsigned) are the coefficients in the expansion
where 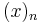 is the Pochhammer symbol for the falling factorial,
is the Pochhammer symbol for the falling factorial,
Note that (x)0 = 1 because it is an empty product. Combinatorialists also sometimes use the notation 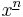 for the falling factorial, and
for the falling factorial, and 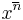 for the rising factorial.[1]
for the rising factorial.[1]
(Confusingly, the Pochhammer symbol that many use for falling factorials is used in special functions for rising factorials.)
Stirling numbers of the second kind
Stirling numbers of the second kind count the number of ways to partition a set of n elements into k nonempty subsets. They are denoted by 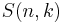 or
or 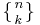 .[2] The sum
.[2] The sum
is the nth Bell number. Using falling factorials, we can also characterize the Stirling numbers of the second kind by
The Lah number, are sometimes being referred as Stirling numbers of the third kind. for example see.
Inversion relationships
The Stirling numbers of the first and second kind can be considered to be inverses of one another:
and
where 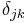 is the Kronecker delta. These two relationships may be understood to be matrix inverses. That is, let s be the lower triangular matrix of Stirling numbers of first kind, so that it has matrix elements
is the Kronecker delta. These two relationships may be understood to be matrix inverses. That is, let s be the lower triangular matrix of Stirling numbers of first kind, so that it has matrix elements
Then, the inverse of this matrix is S, the lower triangular matrix of Stirling numbers of second kind. Symbolically, one writes
where the matrix elements of S are
Note that although s and S are infinite, this works for finite matrices by only considering Stirling numbers up to some number N.
A generalization of the inversion relationship gives the link with Lah numbers 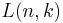
with the conventions 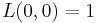 and
and 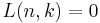 if
if 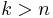 .
.
Symmetric formulae
Abramowitz and Stegun give the following symmetric formulae that relate the Stirling numbers of the first and second kind.
and
See also
- Bell polynomials
- Cycles and fixed points
- Lah number
- Pochhammer symbol
- Polynomial sequence
- Stirling transform
- Touchard polynomials
References
- ^ Aigner, Martin (2007). "Section 1.2 - Subsets and Binomial Coefficients". A Course In Enumeration. Springer. pp. 561. ISBN 3540390324.
- ^ Ronald L. Graham, Donald E. Knuth, Oren Patashnik (1988) Concrete Mathematics, Addison-Wesley, Reading MA. ISBN 0-201-14236-8, p. 244.
- M. Abramowitz, I. Stegun (Eds.). Stirling Numbers of the First Kind., §24.1.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 824, 1972.
- Milton Abramowitz and Irene A. Stegun, eds., Handbook of Mathematical Functions (with Formulas, Graphs and Mathematical Tables), U.S. Dept. of Commerce, National Bureau of Standards, Applied Math. Series 55, 1964, 1046 pages (9th Printing: November 1970) - Combinatorial Analysis, Table 24.4, Stirling Numbers of the Second Kind (author: Francis L. Miksa), p. 835.
- D.E. Knuth, Two notes on notation (TeX source).
- Louis Comtet, Valeur de s(n, k), Analyse combinatoire, Tome second (page 51), Presses universitaires de France, 1970.
- Louis Comtet, Advanced Combinatorics: The Art of Finite and Infinite Expansions, Reidel Publishing Company, Dordrecht-Holland/Boston-U.S.A., 1974.
- Stirling numbers of the first kind, s(n,k) on PlanetMath.
- Stirling numbers of the second kind, S(n,k) on PlanetMath.
- Sloane's A008275 : Stirling numbers of first kind. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Sloane's A008277 : Stirling numbers of 2nd kind. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Francis L. Miksa (1901–1975), Stirling numbers of the first kind, "27 leaves reproduced from typewritten manuscript on deposit in the UMT File", Mathematical Tables and Other Aids to Computation, vol. 10, no. 53, January 1956, pp. 37–38 (Reviews and Descriptions of Tables and Books, 7[I]).
- Dragoslav S. Mitrinović, Sur les nombres de Stirling de première espèce et les polynômes de Stirling, AMS 11B73_05A19, Publications de la Faculté d'Electrotechnique de l'Université de Belgrade, Série Mathématiques et Physique (ISSN 0522-8441), no. 23, 1959 (5.V.1959), pp. 1–20.
- Victor Adamchik, "On Stirling Numbers and Euler Sums", Journal of Computational and Applied Mathematics 79 (1997) pp. 119–130.
- Arthur T. Benjamin, Gregory O. Preston, Jennifer J. Quinn, A Stirling Encounter with Harmonic Numbers, (2002) Mathematics Magazine, 75 (2) pp 95–103.
- J. M. Sixdeniers, K. A. Penson, A. I. Solomon, Extended Bell and Stirling Numbers From Hypergeometric Exponentiation (2001), Journal of Integer Sequences, 4, Article 01.1.4.
- Hsien-Kuei Hwang (1995). "Asymptotic Expansions for the Stirling Numbers of the First Kind". Journal of Combinatorial Theory, Series A 71 (2): 343–351. doi:10.1016/0097-3165(95)90010-1. http://citeseer.ist.psu.edu/577040.html.
- John J. O'Connor, Edmund F. Robertson, James Stirling (1692–1770), (September 1998).
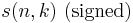
![\left[{n \atop k}\right]=c(n,k)=|s(n,k)|\text{ (unsigned)}\,](/2012-wikipedia_en_all_nopic_01_2012/I/708a35019f1f405b3553f162d775737a.png)
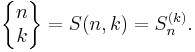
![c(n,k)=\left[{n \atop k}\right]=|s(n,k)|=(-1)^{n-k} s(n,k)](/2012-wikipedia_en_all_nopic_01_2012/I/c41adf282179c1b7c473ea27348ea040.png)
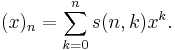
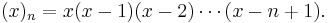
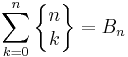
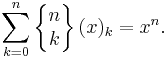
![\sum_{n=0}^{\max\{j,k\}} (-1)^{n-k} \left[{n\atop j}\right] \left\{{k\atop n}\right\} = \delta_{jk}](/2012-wikipedia_en_all_nopic_01_2012/I/d7f7d0f59bc70d3e828d88ce79d102c7.png)
![\sum_{n=0}^{\max\{j,k\}} (-1)^{n-k} \left\{{n\atop j}\right\} \left[{k\atop n}\right] = \delta_{jk}](/2012-wikipedia_en_all_nopic_01_2012/I/84505415784d14de0619baae7193442b.png)
![[s]_{nk}=s(n,k)=(-1)^{n-k} \left[{n\atop k}\right].\,](/2012-wikipedia_en_all_nopic_01_2012/I/cb76f802e710ab2de5040774973e69f6.png)
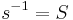
![[S]_{nk}=S(n,k)=\left\{{n\atop k}\right\}.](/2012-wikipedia_en_all_nopic_01_2012/I/13d7309ac5cfb603c78428d04777011b.png)
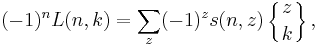
![\left[{n\atop k}\right] = (-1)^{n-k} \sum_{j=0}^{n-k} (-1)^j {n-1%2Bj \choose n-k%2Bj} {2n-k \choose n-k-j} \left\{{n-k%2Bj\atop j}\right\}](/2012-wikipedia_en_all_nopic_01_2012/I/4eb4cf69c5a104a0e2f347ece52dad0e.png)
![\left\{{n\atop k}\right\} = (-1)^{n-k} \sum_{j=0}^{n-k} (-1)^j {n-1%2Bj \choose n-k%2Bj} {2n-k \choose n-k-j} \left[{n-k%2Bj\atop j}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/b63504ad43633616f4747314de744c1a.png)